
چکیده
به دلیل رفتار هیستریک پایدار، استفاده از مهاربندهای کمانش تاب (BRB) در سازههای بتنی جهت توسعه سیستم سازهای دوگانه افزایش یافته است. در این مقاله به دنبال سنجش رفتار لرزهای قابهای بتنی با مهاربند کمانش تاب (RC-BRBF) هستیم.

مهاربندهای کمانش تاب (BRB) به عنوان یک المان سازهای مؤثر جهت مقاومت در برابر نیروی جانبی، کاهش پاسخ لرزهای و مهار انرژی ناشی از کنشهای لرزهای در سازههای مهندسی به صورت گسترده استفاده میشود. مکانیزم پاسخ غیرالاستیک BRB بگونه ایست که بخشهای هستهی فولادی تحت کشش و فشار دچار تسلیم میشوند، و پدیدهی هیسترزیس رامبرگ- اوسگود تحت بارگذاریهای چرخهای به وجود میآید. علاوه بر این، مزایای اقتصادی تولید BRB و استفاده از آن، در هزینههای مصالح و ساخت، و امکان بهسازی لرزهای به نوبه خود جذاب هستند و این ویژگیها BRB را به گزینهای مناسب جهت استفاده در سازههای بتنی تبدیل میکند و با توجه به اینکه BRB ها پاسخ هیستریک عالیای را به نمایش میگذارند، کاربرد آنها در سازههای بتنی به شدت در حال گسترش است. همچنین استفاده از BRBها در سازههای بتنی، به منظور مقاوم سازی لرزهای ساختمانهای موجود و استفاده در ساختمانهای جدیدالاحداث، منجر به افزایش مقاومت و سختی سازه میگردد. در واقع چنین ساختمانهایی از یک سیستم سازهای دوگانه برخوردار هستند که این سیستم ضمن بهبود عملکرد لرزهای، دریفت پسماند را نیز کاهش میدهد. لازم به ذکر است که پژوهشهای زیادی در حوزه طراحی لرزهای سازههای RC-BRBF (سازه بتنی با مهاربند کمانش تاب) انجام شده است که عناوین برخی از آنها آمده است.
نمونه پژوهشها:
1. کیم و همکاران فرآیند طراحی ظرفیت مبتنی بر طیف را برای قابهای خمشی فولادی با استفاده از BRB پیشنهاد کردند.
2. مالی و همکاران با استفاده از روش طراحی مبتنی بر جابه جایی، شیوهای را جهت طراحی BRBF های دوگانه پیشنهاد کردند.
3. اویئدو و همکاران پاسخ لرزهای یک سازهی بتنی مجهز به BRB را به صورت سیستمی مورد بررسی قرار دادند.
4. گوئررو و همکاران یک روش مقدماتی جهت طراحی و ارزیابی لرزهای سازههای کم ارتفاع مجهز به BRB را بر اساس تحلیل پاسخ لرزهای نوسان سازهای دوگانه با یک درجه آزادی (SDOF) توسعه دادند. اساسا به دلیل برهم کنش بین سیستم BRB و سیستم قاب، جهت اندازهگیری نیروهای داخلی (مقادیر قابل تحمل) اجزای بتنی، باید پروسه طراحی لرزهای RC-BRBF ها به صورت یکپارچه درنظر گرفته شود. این در حالیست که روشهای طراحی فعلی، این ویژگی را به صورت سیستمی برای سیستمهای دوگانه در نظر نمیگیرند.

علاوه بر نکات فوق، یک موضوع مهم جهت طراحی و تولید RC-BRBF، تفکیک صحیح سیستم دوگانهی کُلی است. یک استراتژی رایج، استفاده از روش طراحی مبتنی بر سختی است جایی که نیروهای جانبی وارد بر سیستم قاب بتنی و سیستم BRB بر اساس سهم سختی، اختصاص داده میشوند. توجه داشته باشید روشهای طراحی مبتنی بر سختی در اصل جهت طراحی سازههای BRBF فولادی دوگانه معرفی شدهاند.
واقعیت این است که برای سازههای بتنی، سختی عمدتاً بر اساس ابعاد مقاطع عناصر سازه محاسبه میشود در حالی که مقاومت با تحلیل همزمان ابعاد و تقویتهای مقطعی تعیین میشود. بنابراین هنوز مشخص نیست که آیا میتوان از روش مبتنی بر سختی در سازههای RC-BRBF (بتنی با مهاربند کمانش تاب) استفاده کرد یا خیر؟ مطالعهی حاضر روش طراحی جایگزین تحت عنوان نسبت بُرش طبقهای را جهت طراحی سیستم RC-BRBF دوگانه با در نظر گرفتن مکانیزم تسلیم سراسری و رفتار BRB بعد از تسلیم پیشنهاد داده است. مشکل اصلی این روش به نسبت نیروی جانبی لرزهای مربوط میشود که توسط BRB ها تحمل میشود. در همین راستا، استاندارد ASCE 7-10 ، قانون 25 % را برای سیستمهای سازهای RC-BRBF پیشنهاد داده است. مطابق این قانون سازه بتنی به گونه ای طراحی میشود که در برابر حداقل 25 % کُل نیروهای لرزهای مقاومت کند. بر اساس دستورالعمل طراحی لرزهای کشور چین، سیستم BRBF باید به میزان بیش از 50 % لنگر واژگونی کُل طبقهی اول مقاومت کند.
وو و همکاران آزمون میز لرزان را برای مدل RC-BRBF سه طبقه با مقیاس 5:1 انجام دادند. نتایج نشان دادند BRB ها میتوانند حداکثر 34-49 % از بُرش کُل طبقه را سهیم شوند. وو و همکاران فرمول تئوریکی را برای تخمین کران بالای نسبت سطح مقطع BRB بین طبقات مختلف ارائه دادند. اما تا این لحظه به سوال: چطور میتوان نسبت بُرش طبقهای مناسب را برای BRB ها انتخاب کرد به نحوی که بتوان به راهحل بهینهای هم از نظر عملکرد لرزهای و هم از نظر ملاحظات اقتصادی نائل آمد؟ هیچ پاسخ شفاف و مناسبی داده نشده است.
با توجه به ملاحظات فوق، مطالعهی فعلی تلاش نموده نسبت به ارزیابی و سنجش پاسخ لرزهای سیستمهای RC-BRBF دوگانهی جدیدالاحداث پاسخ دهد. باید خاطر نشان کرد روش طراحی فعلی که در دستورالعملها و استانداردها توصیه شده است از تحلیل الاستیک سازهای برای طراحی لرزهای استفاده میکند (ASCE، 2010، آیین نامهی طراحی لرزهای ساختمانها GB 50011-2010). در نتیجه سازههای منطبق با آیین نامه که در معرض زلزلههای شدید قرار میگیرند اغلب پاسخ لرزهای غیرقابل پیشبینیای دارند و مدهای فروپاشی (شکست، خرابی) نامطلوبی را تجربه میکنند که مکانیزم طبقهی نرم یکی از آنهاست. دلیلش این است که پروسه طراحی مبتنی بر آیین نامهی فعلی، در خلال طراحی به “مکانیزم تسلیم” و “تقاضای دریفت غیرالاستیک” توجه نمیکند. بنابراین به منظور پیش بینی و کنترل مکانیزم تسلیم و دریفت طبقهای تحت مخاطرات لرزهای شدید، مقالهی حاضر یک روش جدید طراحی پلاستیک عملکردی با در نظر گرفتن “مکانیزم پس از تسلیم” (PBPD) را برای RC-BRBF ها پیشنهاد کرده است. علاوه بر این، رفتارهای RC-BRBF ها با توجه به تعداد طبقات مختلف، حالتهای مختلف نصب BRB و نسبتهای بُرش طبقهای، به صورت سیستمی ارزیابی شدهاند. نسبت بُرش طبقهای تحمل شده توسط BRBها محاسبه شده است و نسبت بُرش طبقهای طراحی بهینه پیشنهاد شده است.

شرکت پویا تدبیر ویرا (ویرابریس) با سابقه سال ها فعالیت در زمینه طراحی، تولید، تأمین و ترویج فناوریهای نوین لرزهای از جمله جداسازها و میراگرهای لرزهای و با در نظر گرفتن نیاز مبرم صنعت ساخت و ساز کشور به فناوریهای نوین حفاظت سازهها در برابر زمین لرزه، از اواخر سال 1390 موضوع بومیسازی و تولید داخلی تجهیزات کنترل ارتعاشات لرزهای را در دستور کار خود، قرار داده است.
سیستم سازهای RC-BRBF دوگانه
به طور کُلی،پس از تولید BRB ها، آنها به کمک چیدمانهای قطری، V شکل، و V شکل معکوس در سازههای بتنی نصب میشوند. پس از اضافه شدن BRBها به سازه، یک سیستم دوگانه توسعه مییابد و رفتار کُلی سیستم ناشی از تاثیرات BRB و سیستم قاب بتنی است همانطور که در شکل 1 به نمایش گذاشته شدهاند.
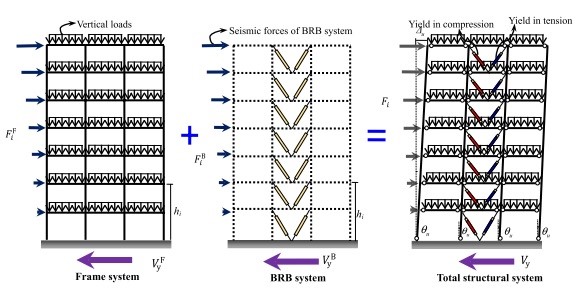
تحمل بارهای عمودی (ثقلی) باید به صورت صد در صدی توسط سیستم قاب انجام شود. این در حالیست که بارهای جانبی لرزهای توسط هر دو سیستم قاب و BRB تحمل میشوند. انتظار میرود تحت بارگذاری لرزهای شدید، مکانیزم تسلیم سراسری کُل سیستم دوگانه جایی که تمام BRB ها دچار تسلیم میشوند و مفصلهای پلاستیک در تمام تیرها و ستونهای اصلی ایجاد میشوند، توسعه یابد. باید توجه نمود که اعضای قاب که BRB ها را متصل میکنند باید مستقیماً در برابر بخشی از بارهای لرزهای جانبی، و نیروهای ایجاد شده در BRBهای در حال تسلیم مقاومت کنند. به طور مشخص باید نیروهای نامتوازن مهاربند را در فرایند طراحی در نظر گرفت. با انجام این کار از شکل گیری مفصل پلاستیک در تیرهای دهانه مهاربندی شده با مهاربند کمانش تاب، به دلیل کُنش مهاربندی در حالتهای V و V معکوس جلوگیری میشود.
منحنی بُرش- جابه جایی ایده آل سیستم RC-BRBF تحت بارگذاریهای لرزهای جانبی با برهم نهی تمام سیستمهای مستقل بدست میآید. همچنین مطابق شکل 2 از منحنیهای ظرفیت دوخطی برای هر سیستم استفاده میشود. در نتیجهی این حالت رابطهی نیرو- تغییرشکل سه خطی برای سیستم سازهای کُل حاصل میشود. در شکل Vy، VyB و VyF به ترتیب نشان دهندهی بُرش پایه طراحی کُل سیستم، BRB و سیستم قاب RC هستند و Vy y= Vy B + Vy F . در بحث طراحی سازه، یک مسئلهی مهم نحوهی تفکیک سیستم دوگانهی کُل به دو سیستم جداگانه است. هدف از این کار تخمین نیروهای داخلی است.
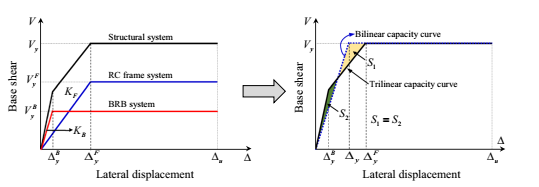
در این مقاله از p (نسبت بُرش طبقهای) جهت اندازهگیری نیروهای جانبی تحمل شده توسط هر سیستم استفاده شد، همچنین p = VBRB/VT که در آن VBRB بُرش طبقهای سیستم BRB و VT بُرش طبقهای سیستم دوگانه کُل هستند. اگر پروفیلهای نیروی جانبی را برای دو سیستم مجزا، یکسان فرض کنیم، بُرش طبقهای هر سیستم برابرست با:

علاوه بر این، منحنی نیرو-جابه جایی سه خطی، با استفاده از رویکرد انرژی محور نشان داده شده در شکل 2 به صورت منحنی ظرفیت دو خطی ایده آل سازی میشود. جابه جایی تسلیم (Δy) سیستم دوخطی نیز اینگونه محاسبه میشود:
که δ = Δ y B / Δ y F ، و Δ y B و Δ y F به ترتیب جابه جایی تسلیم BRB و سیستم قاب هستند.حالت متداول نصب BRB در شکل 3 به نمایش گذاشته شده است. در طراحی BRB ها باید به طول و سطح مقطع هر بخش توجه کرد: طول Lj و مساحت سطح مقطع Aj برای بخش اتصال، طول Lt و مساحت سطح مقطع At برای بخش گذار، و Lc و Ac متناظر برای بخش هسته. بنابراین طول کُل Lw عضو BRB به صورت Lw= 2Lj + 2Lt +Lc محاسبه میشود. با توجه به این پارامترها، نسبت دریفت تسلیم سیستم BRB اینگونه تعیین میشود:
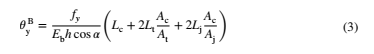
که در آن Eb مدول الاستیک BRB و h ارتفاع طبقه، و α زاویه شیب BRB هستند. برای سیستم قاب RC تنها، اطلاعات دقیق سطح مقطع از ابتدا در دسترس نخواهند بود. نسبت جابه جایی تسلیم ( θyf) به صورت تقریبی بر اساس تحلیل انحنای مقطع مشخص میشود:
که در آن ɛy کرنش تسلیم مسلح سازی ،Lb و hb دهانه و عمق تیر هستند. در این صورت ρ به صورت ρ = θy B / θY F و نسبت دریفت تسلیم به صورت
θy = θy F (1- p + pρ) محاسبه میشوند.


ثبت ديدگاه